Общие сведения о 2D сплайнах |
  
|
Информация в данной главе применима как к сплайнам, относящимся к линиям построения, так и к сплайнам, относящимся к линиям изображения.
Данный раздел содержит математическое описание таких параметров сплайна, как:
•гладкость в точках, привязанных к другим линиям.
Тип параметризации существенно влияет на форму сплайна особенно на участках с близко расположенными точками, меняющими направление кривой.
При изменении типа параметризации одни и те же значения параметров могут соответствовать разным конфигурациям сплайна. Между двумя характерными точками сплайна будет разная длина дуги.
Доступны следующие варианты параметризации сплайна:
•По длине;
По умолчанию для сплайнов используется Центростремительная параметризация.
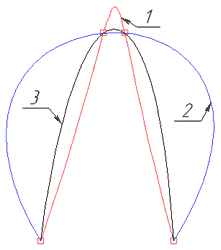
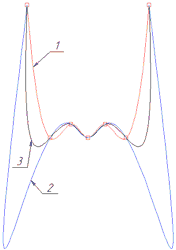
1 – Равномерная; 2 – По длине; 3 – Центростремительная
При изменении положения характерных точек или при добавлении точек параметризация сплайна пересчитывается. Это необходимо при построении или редактировании нового сплайна, поэтому для строящегося или редактируемого сплайна фиксированная параметризация недоступна. В случае если сплайн был разбит, обрезан или импортирован из другой системы, то у него будет фиксированная параметризация. В режиме фиксированной параметризации редактирование сплайна достаточно ограничено. Это связано с тем, что при редактировании изменяется длина дуги, которая приходится на фиксированное значение параметров. При увеличении расстояния между точками могут образовываться плоские участки, а при уменьшении – петли.
При обрезке или разбиении сплайна тип его параметризации автоматически становится фиксированным. Тип параметризации для фиксированного сплайна можно поменять, но тогда его геометрия изменится. В режиме фиксированной параметризации допустимо делать только несущественные корректировки сплайна.
Если разбитый/обрезанный сплайн имеет всего три или две характерные точки, то менять параметризацию с фиксированной на любую другую не рекомендуется. По умолчанию сплайны строятся на основе кубических полиномов, и трёх точек недостаточно для корректного построения кубического сплайна. Надо либо понизить степень сплайна, либо не менять тип параметризации.
В случае если сплайн был разбит или обрезан, то для сохранения геометрии в двух крайних точках сплайна фиксируются первая и вторая производные. Если сплайн необходимо редактировать, то рекомендуется снять фиксацию производных, сняв флаги в параметрах точек.
Параметры распределяется в соответствии с длиной дуг между соседними точками. Дуги между точками являются кривыми построенными на полиномах, т.е. сплайн можно представить, как последовательность таких дуг.
Пусть для построения сплайна заданы характерные точки Dk, где k=0,1,…,n.
Длина всех дуг (длина сплайна) L будет определяться выражением:
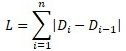
Длина дуг Lk от D0 до Dk:
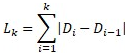
Область определения параметров: t [0,1].
Каждый параметр tk должен соответствовать длине Lk, тогда:
t0=0
|
при k= 0, 1, …, n-1 |
t1=1
Метод параметризации по длине дуги широко распространён и обычно хорошо работает. При этом нужно учитывать, что полиномиальный сплайн между двумя точками не является дугой – его можно принимать за дугу лишь приблизительно. Если дуга длинная, сплайн, построенный по данному типу параметризации, может дать большую выпуклость.
Название метода отражает его физическую интерпретацию. При движении по траектории, представляющей собой сплайн, чем сильнее изгиб, тем больше центростремительная сила. Центростремительная сила пропорциональна изменению угла. Центростремительный метод параметризации является приближением к такой физической модели. С точки зрения математики центростремительный метод параметризации – это модификация метода параметризации по длине.
Пусть для построения сплайна заданы характерные точки Dk, где k=0,1,…,n.
Область определения параметров: t [0,1].
Введём показатель α, который будет модифицировать выражения метода параметризации по длине:
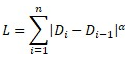
t0=0
|
при k= 0, 1, …, n-1 |
t1=1
Если показатель α=1, то центростремительная параметризация и параметризация по длине дают одинаковый результат построения.
Если показатель α˂1, ![]() и
и ![]() , то влияние более длинной дуги уменьшается. Под влиянием тут нужно понимать величину изменения параметра для соответствующей дуги.
, то влияние более длинной дуги уменьшается. Под влиянием тут нужно понимать величину изменения параметра для соответствующей дуги.
Если показатель α˂1, ![]() и
и ![]() , то влияние короткой дуги увеличивается.
, то влияние короткой дуги увеличивается.
Пусть для построения сплайна заданы характерные точки Dk, где k=0,1,…,n.
Область определения параметров: t [0,1].
Крайние параметры: t0=0 и t1=1.
Другие параметры: 1/n, 2/n,…,(n-1)/n.
При равномерной параметризации, чаще чем в других методах, возможны резкие выпуклости, пики, петли. При этом данный тип параметризации наиболее простой и интуитивно понятный.
Данный метод параметризации доступен для совместимости сплайнов, построенных в T-FLEX CAD 15 и раньше. При создании сплайнов в более поздних версиях T-FLEX CAD лучше пользоваться методами По длине, Центростремительная и Равномерная.
Удлинение позволяет удлинить (при положительном значении) или укоротить (при отрицательном значении) сплайн, добавив или удалив участки в его крайних точках. Удлинение может производиться с использованием различных математических законов. Закон построения добавляемых участков определяется параметром Способ удлинения. Для отрицательных смещений способ удлинения не оказывает влияния на геометрию сплайна.
Доступны следующие способы удлинения.
•По прямой
При данном способе только первая производная представляет собой гладкую функцию. В начальной или конечной точке сплайна строится касательный отрезок прямой. Непрерывность по кривизне не сохраняется.
•С сохранением кривизны
И первая и вторая производные представляют собой гладкие функции. При этом автоматически задаётся плавное уменьшение кривизны до нуля. Т.е. добавляемый участок начинается с такой же кривизны ,как у соседнего участка сплайна, и затем плавно переходит в прямую с сохранением непрерывности по кривизне.
•С отражением
Сплайн отражается симметрично относительно перпендикуляра к касательной построенного в начальной или конечной точке сплайна.
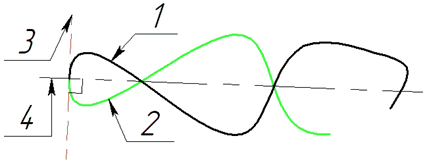
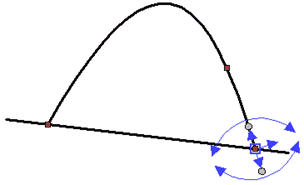
Удлинение с отражением: 1 – исходный сплайн; 2 – добавляемый участок; 3 – касательная в начальной точке; 4 – перпендикуляр к касательной
•По параметру
Непрерывность по кривизне сохраняется, на протяжении всего участка смещения идёт плавное уменьшение кривизны. В конечной точке добавляемого участка кривизна достигает нуля, а радиус кривизны достигает бесконечности.
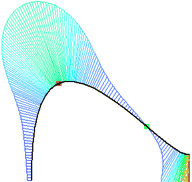
Эпюра кривизны для удлинения по параметру демонстрирует плавное уменьшение кривизны без изломов.
•По дуге
Только первая производная представляет собой гладкую функцию, непрерывность по кривизне не сохраняется. Из начальной или конечной точки сплайна строится касательная дуга окружности, радиус которой равен радиусу кривизны в этой точке.
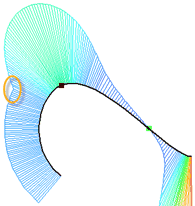
Эпюра кривизны для удлинения по дуге имеет излом.
Гладкость в точках, привязанных к линиям изображения
Если характерная точка сплайна привязана к линии изображения, то можно задать один из трёх вариантов гладкости сплайна в такой точке. Следующие опции гладкости доступны в автоменю и динамической панели при выборе точки:
•G1 – непрерывность по первой производной (по касательной)
В выбранной точке совпадают направления касательных к сплайну и к линии привязки. Это означает, что углы первой производной обеих линий в крайних точках будут либо равны, либо отличаться на число, кратное 180°. Например, построим два последовательных сплайна: последняя точка первого сплайна совпадает с первой точкой второго. Для второго сплайна в первой точке выберем гладкость G1. Углы касательной в последней точке первого сплайна и первой точке второго будут равны.
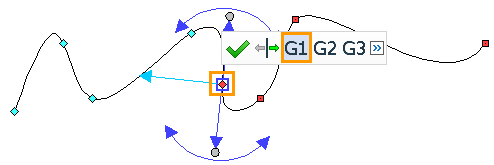
Остальные параметры линий в выбранной точке при использовании гладкости G1 могут отличаться.
Использование гладкости G1 возможно только для сплайнов второй степени и выше.
•G2 - непрерывность по второй производной (по кривизне)
В выбранной точке совпадают направления касательных и центры кривизны сплайна и линии привязки. Т.е., к условию G1 добавляется равенство радиусов кривизны. Например, построим дугу радиусом 35 мм из которой выходит сплайн. Укажем в первой точке сплайна гладкость G2. Значение радиуса кривизны в первой точке сплайна будет равно 35 мм. Кроме того, если построить касательную в крайней точке дуги, то можно убедиться, что её направление будет совпадать с направлением касательной сплайна, т.к. угол построенной касательной равен углу первой производной в первой точке сплайна.
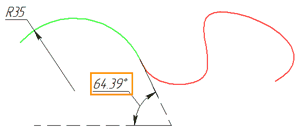
Знак радиуса кривизны отражает направление закручивания сплайна. В случае, когда сплайн и кривая привязки, имеют различное направление закручивания, при использовании гладкости G1 точка изменения знака (точка перегиба в случае непрерывности) функции кривизны находится в крайней точке сплайна. При использовании гладкости G2 точка перегиба сместится внутрь сплайна, а на сам сплайн будет добавлен изгиб с тем же направлением закручивания, что и у кривой привязки. Это необходимо для выполнения условия совпадения центров кривизны линий в выбранной точке. Для примера рассмотрим два последовательных сплайна. Последний участок первого сплайна закручен по часовой стрелке, первый участок второго – против. Выведем для этих сплайнов эпюру кривизны при помощи команды ![]() Кривизна кривых:
Кривизна кривых:
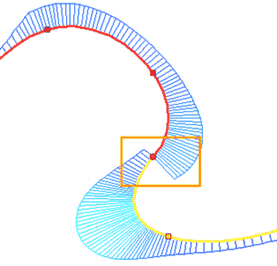
Из эпюры видно, что в последней точке первого сплайна и первой точке второго сплайна функция кривизны меняет знак, причём в данном случае с разрывом функции.
Применим для последней точки первого сплайна гладкость G2. Из эпюры видно, что точка перегиба сместилась внутрь первого сплайна: на первый сплайн был добавлен небольшой участок с направлением закручивания как у второго сплайна.
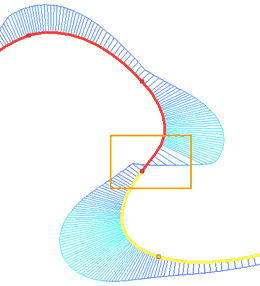
Нужно отметить, что функция кривизны стала непрерывной, однако в крайних точках гладкость функции кривизны нарушается. Для сохранения гладкости функции кривизны в крайних точках сплайна существует третий вариант гладкости.
Использование гладкости G2 возможно только для сплайнов третьей степени и выше.
•G3 - непрерывность по третьей производной
В выбранной точке совпадают направления касательных, центры кривизны и направления касательных к функции кривизны для сплайна и линии привязки. Т.е., к условиям G1 и G2 добавляется условие гладкости функции кривизны. Продолжим рассмотрение предыдущего примера с двумя последовательными сплайнами. Выберем для крайней точки первого сплайна вместо гладкости G2 гладкость G3. Из рисунка видно, что при использовании гладкости G3 функция кривизны сохраняет гладкость в крайних точках сплайнов.
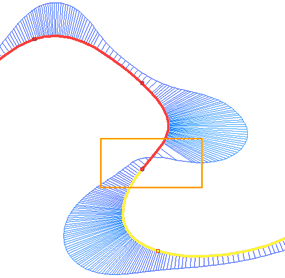
Использование гладкости G3 возможно только для сплайнов четвёртой степени и выше. Если у сплайна степень ниже чем четвёртая, то при выборе гладкости G3 степень сплайна будет автоматически повышена до четвёртой.
Если рассматривать гладкости G1, G2, G3 с точки зрения их влияния на функцию кривизны, то можно сформулировать следующее правило:
G1 – функция кривизны не сохраняет непрерывность в выбранной точке;
G2 – функция кривизны непрерывная, но не сохраняет гладкость в выбранной точке;
G3 – функция кривизны непрерывная и сохраняет гладкость в выбранной точке.
|
|
|
G1 |
G2 |
G3 |
См. также: